Pepper: toward practical verifiable computation

Elevator pitch

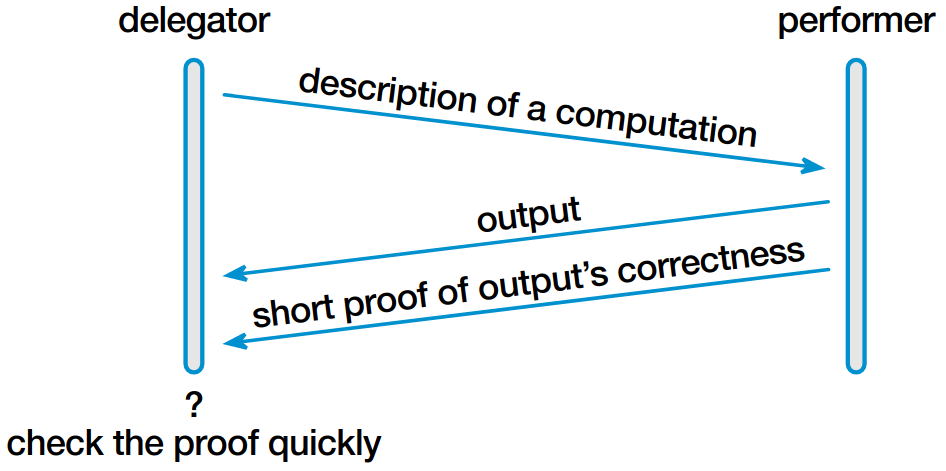
The Pepper project at NYU and UT Austin is tackling the problem of verifying outsourced computations. Our approach is to reduce to practice powerful tools from complexity theory and cryptography: probabilistically checkable proofs (PCPs), efficient arguments, etc.

Highlights of the project’s results include:

  • improving the performance of a PCP-based efficient argument by a factor of 1020
  • broadening the computational model used in verifiable computation: from Boolean circuits to a general-purpose model
  • extending verifiability to representative uses of cloud computing: MapReduce jobs, simple database queries, interactions with private state, etc.
  • a series of built systems that implement the aforementioned refinements, with the following features:
    • GPU acceleration
    • a compiler that allows the developer to express a computation in a restricted subset of C; the compiler produces executables that implement the protocol entities
  • Verifiable ASICs, a new approach to building trustworthy hardware using untrusted components

Though these systems are not yet at true practicality, they are arguably practical in some regimes. More importantly, these systems highlight the potential applicability of the theory, and indeed, there is now a thriving research area based on this promise. Thus, we are hopeful that over the next few years, the underlying theoretical tools will find their way into real systems.

Overview: what is Pepper?

Pepper is an academic research project whose goal is to make verified computation practical. By verified computation (which is sometimes also called “verifiable computation”), we mean a system that implements the following picture:

Overview of Pepper

One motivation is cloud computing (more generally, third-party computing). These environments bring:

  • Issues of scale: with hundreds of thousands or millions of machines, correct and unfailing execution in all cases seems unlikely.
  • Issues of trust: the computation “provider” and the “consumer” are different entities.

Goal: A system that is

  1. Comprehensive -- the system makes no assumptions about the behavior and capabilities of the performing computer other than cryptographic hardness.
  2. General-purpose -- not specialized to a particular family of functions.
  3. Practical -- can be used for real problems.

Prior work does not meet all three of these properties.

We approach this problem using deep results in cryptography and complexity theory. Here is a high-level description of the foundations of our approach.

Our approach: PCPs, argument systems, and interactive proofs

Our approach is to apply the fascinating theory of Probabilistically Checkable Proofs (PCPs) and two closely related constructs: argument systems and interactive proofs.

The theory surrounding PCPs demonstrates, astonishingly, that it is possible (in principle) to check a mathematical proof by investigating only a few bits of that proof. In our context, this implies that the picture we wanted has a solution, one that is unconditional and general-purpose.

The research: make the theory practical

Unfortunately, PCPs, as described in the theoretical literature, are not remotely practical: in the most asymptotically “efficient” schemes, the server would take trillions of years to produce a proof.

Can we incorporate PCPs into a built system? So far, we have been able to come close. Here is a top-level summary of Pepper’s results to date.

Summary of Pepper’s results so far

Our line of work on Pepper, Ginger, and Zaatar has instantiated an argument system (an interactive protocol that assumes a computationally bounded prover) due to Ishai, Kushilevitz, and Ostrovsky (CCC 2007), in this paper (also available here). Through theoretical and practical refinements, we have reduced the cost of this argument system by a factor of roughly 1020 (seriously).

In another line of work, Allspice, we have built on an interactive proof system due to Goldwasser, Kalai, and Rothblum (STOC 2008), and refined and implemented by Cormode, Mitzenmacher, and Thaler (ITCS 2012). One of the chief advantages of this line of work is that it avoids expensive cryptographic operations.

One might wonder: which protocol is “best”? Our experience has been that it depends on the computation. Accordingly, Allspice includes a compiler that takes as input a high-level programming language and performs static analysis to compile to the best available protocol for that computation.

In the above works, the computational model does not support stateful computations, namely those that work over RAM, or computations for which the verifier does not have the full input. In Pantry, we overcome this limitation, and apply the verification machinery to MapReduce jobs, queries against remote databases, and applications for which the prover’s state is private.

Here is a system-by-system description.

Built systems under the Pepper project

In the descriptions below, the prover is the entity that performs a computation. The verifier checks a proof (produced by the prover) that the computation was performed correctly.

Pepper
Pepper is the first system to challenge the folklore that PCP-derived machinery is impractical. Pepper implements an efficient argument system based on a protocol of Ishai et al., CCC 2007, and incorporates new theoretical work to improve performance by 20 orders of magnitude. Pepper is implemented and experimentally evaluated, and is arguably practical for some computations and in some regimes.
S. Setty, R. McPherson, A. J. Blumberg, and M. Walfish, “Making argument systems for outsourced computation practical (sometimes)”, Network & Distributed System Security Symposium (NDSS), February 2012. [pdf]
Ginger
Ginger is based on Pepper. It slashes query costs via further refinements. In addition, Ginger broadens the computational model to include (primitive) floating-point fractions, inequality comparisons, logical operations, and conditional control flow. Ginger also includes a parallel GPU-based implementation, and a compiler that transforms computations expressed in a high-level language to executables that implement the protocol entities.
S. Setty, V. Vu, N. Panpalia, B. Braun, A. J. Blumberg, and M. Walfish, “Taking proof-based verified computation a few steps closer to practicality”, USENIX Security Symposium, August 2012. [pdf (corrected)]
Zaatar
Zaatar addresses a limitation in Ginger, namely that avoiding immense work for the prover requires computation-specific tailoring of the protocols. Zaatar is built on our observation that the QAPs of Gennaro et al., EUROCRYPT 2013 yield a linear PCP that works with the Ginger/Pepper/IKO framework and is (relatively) efficient for the prover. The consequence is a prover whose total work is not much more than linear in the running time of the computation (and does not require special-purpose tailoring).
S. Setty, B. Braun, V. Vu, A. J. Blumberg, B. Parno, and M. Walfish, “Resolving the conflict between generality and plausibility in verified computation”, ACM European Conference on Computer Systems (EuroSys), April 2013. [pdf]
Allspice
Allspice addresses a key limitation of prior work for verifying computations: either it relies on cryptography, which carries an expense (as with Zaatar, Ginger, Pepper, and IKO), or else it applies to a restricted class of computations (as with work by Cormode et al., ITCS 2012, which builds on an interactive proof system of Goldwasser et al., STOC 2008). Allspice optimizes the non-cryptographic protocols and extends them to a much larger class of computations. Allspice also uses static analysis to compile an input program to the best verification machinery for that program.
V. Vu, S. Setty, A. J. Blumberg, and M. Walfish, “A hybrid architecture for interactive verifiable computation”, IEEE Symposium on Security and Privacy (Oakland), May 2013. [pdf]
Pantry
Pantry extends verifiable computation to handle stateful computations: those that work over RAM, or computations for which the verifier does not have the full input. Pantry composes techniques from untrusted storage with existing verifiable computation machinery: the verifier’s explicit input includes a digest of the full input or state, and the prover is obliged to compute over state that matches the digest. The result is to extend verifiability to real applications of cloud computing (MapReduce jobs, queries against remote databases, applications for which the prover’s state is hidden, etc.). Besides the gain in expressiveness, Pantry improves performance: by not handling inputs, the verifier saves CPU and network costs.
B. Braun, A. J. Feldman, Z. Ren, S. Setty, A. J. Blumberg, and M. Walfish, “Verifying computations with state”, ACM Symposium on Operating Systems Principles (SOSP), November 2013. [pdf]
Buffet
Buffet eliminates what was a problematic cost-programmability tradeoff in this research area. Prior to Buffet, there were two approaches to program representation. One approach, due to Ben-Sasson et al., Usenix Security 2014, offered excellent programmability (the full C programming language) but substantial overhead. Another approach (embodied by Pantry, Pinocchio, and Zaatar) offered much lower overhead but could not handle data-dependent control flow. Buffet takes Pantry as a base and applies static program analysis (including loop flattening) together with an adaptation of BCTV's elegant representation of RAM. Buffet can handle essentially any example in the verifiable computation literature (it supports an expansive subset of C, disallowing only goto and function pointers) and achieves the best performance in the area by multiple orders of magnitude.
R. S. Wahby, S. Setty, Z. Ren, A. J. Blumberg, and M. Walfish, "Efficient RAM and control flow in verifiable outsourced computation." Network & Distributed System Security Symposium, NDSS 2015, February 2015. [pdf]
A slightly longer version is available as Cryptology ePrint 2014/674.
Zebra
Zebra instantiates a new model for building trustworthy chips, called Verifiable ASICs. This model uses a high-performance chip from an untrusted (and possibly malicious) hardware vendor to accelerate the computation of a low-performance chip supplied by a trusted vendor, while retaining the latter's trustworthiness. To instantiate the model, Zebra builds on the interactive proofs of GKR, CMT, and Allspice. Zebra demonstrates that, for a class of real computations, the Verifiable ASICs approach reduces costs and improves performance compared to chips built solely by a trusted manufacturer.
R. S. Wahby, M. Howald, S. Garg, a. shelat, and M. Walfish, "Verifiable ASICs." IEEE Symposium on Security and Privacy (Oakland), May 2016. [pdf] (Distinguished student paper award.)
An extended version is available as Cryptology ePrint 2015/1243.
Giraffe
Giraffe builds on the Verifiable ASICs model introduced by Zebra. Giraffe removes Zebra's requirement that a trusted entity supply the verifier with an endless stream of precomputations. In doing so, it charges for all protocol costs and makes outsourcing with probabilistic proofs worthwhile for the first time.

Giraffe includes a new probabilistic proof for data-parallel computations that refines the protocol of Thaler13 to give asymptotically optimal prover cost; this is of independent interest. Giraffe also develops a design template that automatically produces optimized hardware designs for a wide range of computations and circuit technologies. It combines this template with program analysis and compiler techniques that extend the Verifiable ASICs model to a wider range of computations. Compared to Zebra, Giraffe handles computations that are 500× larger, and it can automatically outsource parts of programs that are not worthwhile to outsource in full.

R. S. Wahby, Y. Ji, A. J. Blumberg, a. shelat, J. Thaler, M. Walfish, and T. Wies, "Full accounting for verifiable outsourcing." ACM Conference on Computer and Communications Security (CCS), October 2017. [pdf]
An extended version is available as Cryptology ePrint 2017/242.
Here is a summary of the performance of the above systems.

Summary of performance

Here is a high-level summary. (Our publications provide detail. See especially this CACM article and Buffet.)

None of our systems (or the others in this area) have achieved true practicality yet.

There are two principal issues, for all of these projects:

(1) Costs to the verifier. To check that a remote computation was performed correctly, the verifier must incur a per-computation setup cost: this cost (which consists of CPU and network costs) amortizes over multiple instances of the same computation (potentially over all future instances), on different inputs. However, the cross-over point, in terms of when the setup cost is paid for, is quite high: tens or hundreds of thousands of instances of the same computation.

  • This setup cost can be slashed (as in Allspice) or eliminated (as in CMT). Unfortunately, these solutions apply only to restricted classes of computations.
  • Using the techniques of BCTV, the setup cost can be reused over all computations of the same size. However, the cost of these techniques is very high, and in practice, one would need to incur the setup cost thousands of times anyway (as explained in Buffet).
  • Using other techniques of BCTV, the setup cost can be made independent of the computation. However, these techniques are primarily theory at this point; for example, the prover's computational costs are many orders of magnitude higher than the other works in the area.

(2) Costs to the prover. The CPU costs to the prover are currently immense: orders of magnitude (factors between a thousand and a million) more than simply executing the computation. An additional bottleneck is memory: the prover must materialize a transcript of a computation's execution.

As a consequence of the above costs, all projects in this area are currently limited to small-scale computations: programs that take several million steps, but not more.

Publications

  • Doubly-efficient zkSNARKs without trusted setup [pdf]
    Riad S. Wahby, Ioanna Tzialla, abhi shelat, Justin Thaler, and Michael Walfish
    IEEE Symposium on Security and Privacy, Oakland 2018, San Francisco, CA, May 2018.
    An extended version is available as Cryptology ePrint 2017/1132.
  • Full accounting for verifiable outsourcing [pdf]
    Riad S. Wahby, Ye Ji, Andrew J. Blumberg, abhi shelat, Justin Thaler, Michael Walfish, and Thomas Wies
    ACM Conference on Computer and Communications Security, CCS 2017, Dallas, TX, October 2017.
    An extended version is available as Cryptology ePrint 2017/242.
  • Verifiable ASICs [pdf] (Distinguished student paper award.)
    Riad S. Wahby, Max Howald, Siddharth Garg, abhi shelat, and Michael Walfish
    IEEE Symposium on Security and Privacy, Oakland 2016, San Jose, CA, May 2016.
    An extended version is available as Cryptology ePrint 2015/1243.
  • Efficient RAM and control flow in verifiable outsourced computation [pdf]
    Riad S. Wahby, Srinath Setty, Zuocheng Ren, Andrew J. Blumberg, and Michael Walfish
    Network & Distributed System Security Symposium, NDSS 2015, San Diego, CA, February 2015.
    A slightly longer version is available as Cryptology ePrint 2014/674.
  • Verifying computations without reexecuting them: from theoretical possibility to near practicality [link]
    Michael Walfish and Andrew J. Blumberg
    (This survey is written for a general CS audience and is probably a good first paper to read for those curious about the area.)
    Communications of the ACM (CACM), Volume 58, Number 2, pages 74–84, February 2015.
    Prior versions: November 2013, July 2014. (ECCC TR13-165).
  • Verifying computations with state [pdf, extended version]
    Benjamin Braun, Ariel J. Feldman, Zuocheng Ren, Srinath Setty, Andrew J. Blumberg, and Michael Walfish
    ACM Symposium on Operating Systems Principles, SOSP 2013, Farmington, PA, November 2013
  • A hybrid architecture for interactive verifiable computation [pdf]
    Victor Vu, Srinath Setty, Andrew J. Blumberg, and Michael Walfish
    IEEE Symposium on Security and Privacy, Oakland 2013, San Francisco, CA, May 2013
  • Resolving the conflict between generality and plausibility in verified computation [pdf, extended version]
    Srinath Setty, Benjamin Braun, Victor Vu, Andrew J. Blumberg, Bryan Parno, and Michael Walfish
    ACM European Conference on Computer Systems, EuroSys 2013, Prague, Czech Republic, April 2013
  • Taking proof-based verified computation a few steps closer to practicality [pdf (corrected), extended version]
    Srinath Setty, Victor Vu, Nikhil Panpalia, Benjamin Braun, Andrew J. Blumberg, and Michael Walfish
    USENIX Security Symposium, Security 2012, Bellevue, WA, August 2012
  • Making argument systems for outsourced computation practical (sometimes) [pdf]
    Srinath Setty, Richard McPherson, Andrew J. Blumberg, and Michael Walfish
    Network & Distributed System Security Symposium, NDSS 2012, San Diego, CA, February 2012
  • Toward practical and unconditional verification of remote computations [pdf]
    Srinath Setty, Andrew J. Blumberg, and Michael Walfish
    Workshop on Hot Topics in Operating Systems, HotOS 2011, Napa Valley, CA, May 2011

Presentations

Tutorials with exercises
  • Overview of "practical" probabilistic proofs
    This surveys the landscape of "practical" probabilistic proofs.
    slides (610 kB), video
  • Linear PCPs and the role of Quadratic Arithmetic Programs (QAPs)
    This tutorial reviews linear PCPs, which are at the heart of many "practical" probabilistic proofs.
    slides and exercises (732 kB), video
  • Folklore arithmetization of programs
    This tutorial explains how various program constructs (conditionals, equality tests, inequalities, etc.) are represented as systems of equations over a finite field.
    slides and exercises (2 MB), video
    (Owing to a production error, the slide video is out of sync with the rest of the presentation.)

In these slides, grey boxes are explicit exercises.

The slides also contain "blanks" that the presentation fills in, by writing on the slides. You can either try to fill these in as further exercises, or watch the videos.

These presentations are all excerpts from the 2016 Bar-Ilan Winter School on Verifiable Computation.

Comprehensive survey of proofs, arguments, and zero knowledge
This comprehensive survey by Justin Thaler covers probabilistic proofs, with emphasis on "practical" protocols.

People

Project members:

Current and former collaborators:

Source code for all of our built systems is available online, under a BSD-style license. In addition, we provide full re-implementations of most of the related systems; this facilitates performance comparisons.

Implemented systems

We maintain a github repository with our latest released code. For experimenting or building on our work, we suggest using this release. We also maintain a slightly simplified (but still feature-rich) codebase, Pequin. If you want to get started quickly, Pequin is a good choice.

We also provide snapshots of our systems at the time of publication, useful for reproducing our results:

Our systems rely on a number of third-party packages. We provide an archive of versions of these packages that are known to work with our system.

Re-implementations of related systems
  • CMT (included with Allspice and in our latest development branch)
  • Pinocchio (included with Pantry, Pantry-enhanced, Buffet, and our latest development branch)
  • TinyRAM (link; also included with Buffet and as a git submodule in our latest development branch)

HOWTOs are included with all of the source code.

Please contact srinath at cs dot utexas dot edu for questions, updates, and bug fixes.

Funding and support

We are grateful for the support of:

  • DARPA (under award HR0011-20-2-0022)
  • the Air Force Office of Scientific Research (under Young Investigator award FA9550-10-1-0073 and grant FA9550-15-1-0302)
  • the National Science Foundation (under CAREER award 1055057, FIA grant 1040083, CNS-1423249, and CNS-1514422)
  • the Office of Naval Research (under grants N00014-16-1-2154 and N00014-14-1-0469)
  • the Sloan Foundation (under a Sloan Fellowship)
  • Intel Corporation (under an Early Career Faculty Award)

The opinions and findings are the researchers’ alone.

Please get in touch with comments, questions, etc.

Our email alias is [email protected].